Huffman coding, like Arithmetic Coding, is an algorithm which attempts to compress a sequence of inputs based on the frequency that each input in the sequence occurs. This is made possible because it is often the case that some symbols in an input sequence occur more frequently than others. As such, we can represent symbols that occur more often with a shorter sequence of bits, at the expense of needing to use a longer sequence of bits to represent less frequent symbols. Take the following sentence as an example:
this_is_an_example_sentence_to_help_teach_you_about_compression
The spaces have been replaced with underscores for clarity. From this, we can count the number of times each character occurs:
| Symbol | Frequency |
|---|---|
| _ | 10 |
| e | 8 |
| o | 5 |
| s | 5 |
| t | 5 |
| a | 4 |
| n | 4 |
| c | 3 |
| h | 3 |
| i | 3 |
| p | 3 |
| l | 2 |
| m | 2 |
| u | 2 |
| b | 1 |
| r | 1 |
| x | 1 |
| y | 1 |
As we can see, the most common symbol is the _, which occurred 10 times, followed by E at 8 occurrences. Typically, ASCII characters are each represented by 8 bits (that is, a sequence of 8 1's and 0's) in binary, which allows for 256 different characters in total. The above string has a length of 63 characters, and therefore using this encoding would take up 8 x 63 = 504 bits.
Given that we only use 18 characters, we could instead represent the above string using 5 bits per character (which would in fact allow for 32 different characters in total). This reduces the length of the string to 5 x 63 = 315 bits. But, given that each character is not used an equal amount of times, we could do even better by representing the _ and E character with fewer bits and, as a compromise, the infrequent characters such as X and Y with more bits. On balance, this would save more bits than it would cost. But how?
Enter Huffman Coding
Invented by David Huffman in 1952, Huffman Coding is one such way of converting symbols and their associated frequencies into sequences of bits, whereby more frequent characters are represented by fewer bits than less frequent characters. The steps are actually quite simple, and are summarized as follows:
Begin with list of all symbols and their associated frequencies
Find the 2 symbols with the lowest frequency
Create a new symbol and link it to these two symbols
Remove the original symbols from the list
Give the new symbol the combined frequencies of the two characters
Add the new symbol to the list
Repeat until only 1 symbol remains in the list
Essentially, these steps are used to create a tree of nodes which ends in the original symbols (or, characters) in the list. Given that the list is sorted by frequency, a tree can be created in linear time by performing the following steps:
Place all symbols into a stack in order of frequency (lowest at the top)
Create an empty queue (created notes will be added to this)
While the queue and stack combined contain more than 1 node
Examine the front of the stack and queue
Remove the lowest frequency item A
Examine the front of the stack and queue
Remove the lowest frequency item B
Create a new node C, with A and B as its children
Set the frequency of C to that of A and B combined
Add this new node to the back of the queue.
The remaining node in the queue or stack is the root node
Here, a stack is simply a structure for storing items wherein the last item you add is the first one taken off. A queue is similar except items can be added or removed from either side. Worth noting is that the order of A and B as the children of a node is important. Conventionally, A would always be on the left, and B on the right.
So, what actually happens here? Well, each time two nodes are linked together, it takes an additional branch to get to either of them. Thus, by linking together the least frequent symbols first, we are increasing the number of bits required to represent them. As a result however, we are also decreasing the number of bits required to represent more frequently occurring symbols, as they are linked together last, and thus are closer to the root of the tree (the final node left in the queue or stack).
Applying this algorithm to the example phrase above, we end up with a tree looking like this:
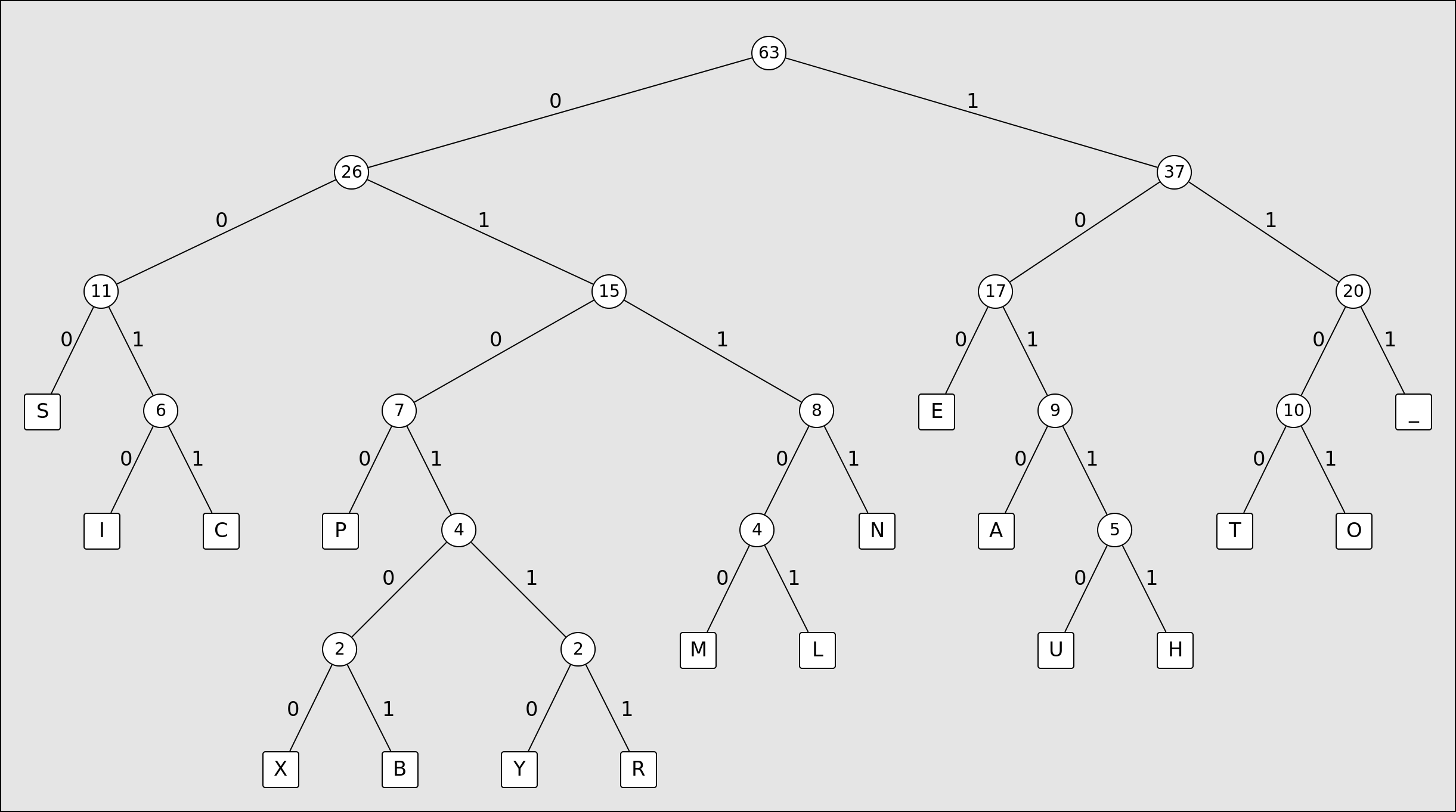
Now, by traversing the tree and noting down the bit on each branch of the tree (0 if you take the left branch and 1 if you take the right branch) until you reach your desired character, you can construct the code used to represent that character. For example, in the tree above the letter E is equal to the bit string 100 and the letter R is equal to 010111. If we do this for every character in the example sentence, appending the bits to each-other until every character in the string has been encoded, we end up with 246 bits, down from the 315 bits required if we use 5 bits to represent each character. This string of bits can be converted back into the original sentence by traversing the tree until we reach a character, and then making note and repeating this process until all of the bits have been read.
Making use of Huffman coding as a means to transmit compressed messages also requires us to encode the generated tree - or the information required to reconstruct it - which of course will take a certain number of bits to represent. If you have a small number of symbols, say the alphabet, you can just encode the frequency that each symbol occurs in alphabetical order. Then, on the other end you can match each frequency back up to a letter in the same order, and reconstruct the tree from that. An even more efficient approach is called Canonical Huffman Coding, in which, as long as the symbols to be transmitted are fixed, you can modify the normal Huffman Coding such that you only need to transmit the length of each bit string that has been produced.
On the other hand, if you do not know which symbols will be transmitted beforehand, and the potential symbol space is quite large (in other words, there are a lot of possible symbols you may transmit, but many of them won't be used in a given message), you will probably have to stick with transmitting each symbol alongside its frequency. In combining Huffman Coding with the Sequitur algorithm as part of my compression project, this is what I had to do.
If you want to avoid transmitting the tree altogether, you must agree on one beforehand with the recipient of your coded message. As an example, you may create a tree based on the average frequency that each letter appears in a given language. This would be fixed and unable to adapt to changes in the frequency of occurrence of different letters.
Summary
Huffman coding is a very simple technique for compressing a given sequence of symbols into fewer bits than would ordinarily be required to represent them if a fixed bit length was used. It is easy to implement, but in actual use you'll probably need to decide on a method of encoding the tree as well as the message coded by it. Finally, it's worth noting that it works particularly well when combined with other methods of compression (Sequitur is one such method) which work to eliminate repetition.
Thanks for reading, and take care! If you would like to know more, let me know!